Statement II is not a correctUse binomial theorem ( a − b) 2 = a 2 − 2 a b b 2 to expand ( x − 2) 2 fx=9\left (x^ {2}4x4\right) ∣ f ∣ x = 9 − ( x 2 − 4 x 4) To find the opposite of x^ {2}4x4, find the opposite of each term To find the opposite of x 2 − 4 x 4, find the opposite of each term fx=9x^ {2}4x4Now suppose that x1,x2 ∈ Z and f(x1) = f(x2) Then x1 5 = x2 5 and thus x1 = x2 It follows that f is onetoone Consequently, f is a bijection Notice that if a function f X → Y is a onetoone correspondence, then it associates one and only one value of y to each value in x In particular, it makes sense to define a reverse function
Solved Question 1 Let F X Sin 1 X 2 Then The Second Derivative At X 1 F 1 Equals A 2 3sqrt3 B 1 4sqrt3 C 2 Sqrt39 D Sqrt6 9 E Course Hero
Let f(x 1/x)=x^2 1/x^2 then f(x) is
Let f(x 1/x)=x^2 1/x^2 then f(x) is-It has been provided or mentioned that a function F(x1)=x^2–3x2 Interestingly, if we substitute a value of x1 in the place of x, we obtain, F((x1)1)=F(x) Therefore, F(x)=(x1)^2–3(x1)2=x^2–2x1–3x32=x^2–5x6 Hence, the function F(x) canM 2, and M 3 be metric spaces Let gbe a uniformly continuous function from M 1 into M 2, and let fbe a uniformly




Section 2 7 One To One Functions And Their Inverses Pdf Free Download
2) If fn → f uniformly on E, then fn → f pointwise on E The sequence f n ( x )= x n on 0 , 1 discussed in Example 1 of the previous section shows thatStatement II is a correct explanation of Statement I (c) Statement I is true, Statement II is true;1 1 and a = b = 2, then we see that a (b ~u) = 2 2 1 1 = 2 4 4 = 16 16 while (ab) ~u = 4 1 1 = 8 8 so we see that a (b ~u) 6= ( ab) ~u (c) V is the set of functions from R to the positive real numbers that is, V is the set of functions f with domain R such that f(x) > 0 for all x 2R Let f and g be in V We de ne f g and c f by de ning
(b) Pick = 1 Given any >0, pick x>0 such that 3 x2 2 >1 Then d(x 2;x) < but we have d(f(x 2);f(x)) = j(x 2)3 x3j= j 3 x2 2 3 2x 22 3 23 j 3 x2 2 >1 This shows that f(x) = x3 is not uniformly continuous on R 445 Let M 1;If f (x) = x1/x1 then find the value of f (2x) Find the answer to this question along with unlimited Maths questions and prepare better for JEE examination31 Continuity 23 so given ϵ > 0, we can choose δ = √ cϵ > 0 in the definition of continuity To prove that f is continuous at 0, we note that if 0 ≤ x < δ where δ = ϵ2 > 0, then f(x)−f(0) = √ x < ϵ Example 38 The function sin R → R is continuous on R To prove this, we use the trigonometric identity for the difference of sines and the inequality sinx ≤ x
Distinct solutions c 1;c 2 and c 3 and nally once more to conclude that f000(x) = 0 has at least two solutions d 1 and d 2 Next, note that since f is a quartic polynomial, f0must be a cubic, f00must be a quadratic and f000must be a linear polynomialWe therefore have a linearX0= 2 1 1 3 x et t 1 This becomes the equations x0 1= 2x x 2 tet x0 2= x 1 3x et 9416 Determine whether the given vector functions are linearly dependent or independent on the interval (1 ;1) sint cost ; Explanation By definition of the derivative f '(x) = lim h→0 f (x h) − f (x) h So with f (x) = 1 x2 we have;



Answered Let F Be A Mapping From 1 0 To Bartleby




Let F X X 1 X N 1 N For Ngeq2 And G X F Ofo Of X Then Intx N 2 G X Dx Equals
Let f (x) = (x 1)2 1, x ≥ 1 Statement I The set {x f (x) = f1(x)} = {0, 1} Statement II f is a bijection (a) Statement I is false, Statement II is true (b) Statement I is true, Statement II is true;Let f x = x x then f '0 is equal to1 0 1 2 Please scroll down to see the correct answer and solution guideOf course, the simple answer would be to just write ( x − 2) for every x you see The answer would be f ( x − 2) = ( x − 2) 2 − 3 ( x − 2) 1 f ( x − 2) = x 2 − 4 x 4 − ( 3 x − 6) 1 f ( x − 2) = x 2 − 4 x 4 − 3 x 6 1 f ( x − 2) = x 2 − 7 x 11




If F X 1 X X 3 1 X 3 4 X 2 1 X 2 13 Then The Value Of F 2 3 Brainly In



Http Www Mast Queensu Ca Math121 Assignmentsolutions Old Sol 05 S03 9 Qa Pdf
Sin2t cos2t We compute the Wronskian det sint sin2t cost cos2t = sintcos2t sin2tcost= sint where the last step can be deduced byAnswer to Let f(x) = (x^2 3x 5)(sqrt(x) 1/fifth root of x) Find f'(x) By signing up, you'll get thousands of stepbystep solutions toGiven a function g with this property, we can easily construct a suitable f Just let f ( x) = { g ( x) x ≥ 0 g ( − x) x < 0 If g is additionally continuous then so is f We can find a lot of continuous g Pick a 1 ∈ ( 0, 1), let a 0 = 0 and recursively a n = a n − 2 2 1 for n ≥ 2




If The Function F R 1 1 To A Definded By F X X 2 1 X 2 Is Surjective Youtube




Section 2 7 One To One Functions And Their Inverses Pdf Free Download
Get an answer for '`f(x) = x/(x^2 1)` (a) Find the intervals on which `f` is increasing or decreasing (b) Find the local maximum and minimum values of `fLet p ∈ Z be any prime We will show that hx2 1i is properly contained in hx2 1,pi which is not equal to Zx This will prove that hx2 1i is not maximal Since every nonzero element of hx2 1i has degree at least 2, p 6∈ hx2 1i This proves that hx2 1i is properly contained in hx2 1,pi Now suppose, for the sake of contradiction, that hx2 1,pi = ZxIf we look at the behaviour as x approaches zero from the right, the function looks like this \begin{matrix}x & f(x) = \frac{1}{x^2} \\ 1 & 1 \\ 01 & 100 \\ 001 & \\ 0001 & \\ & \end{matrix}



Www Portnet Org Cms Lib6 Ny Centricity Domain 276 1st and 2nd derivative test 1 Pdf



Www Iitrpr Ac In Ma101 Ma101 Tutorial sheet 5 Pdf
X Well begun is half done You have joined No matter what your level You can score higher Check your inbox for more details {{navliveTestEngineeringCount}} Students Enrolled {{navliveTestMedicalCount}} Students Enrolled Start Practicing6041/6431 Spring 08 Quiz 2 Wednesday, April 16, 730 930 PM SOLUTIONS Name Recitation Instructor TA Question Part Misc 6 Let f = {("x, " 𝑥2/(1𝑥2)) x ∈ R } be a function from R into R Determine the range of f f = { ("x , " 𝑥2/(1𝑥2)) x ∈ R } We find different values of 𝑥2/(1 𝑥2) for different values of x Domain Value will always be between 0 & 1 We note that Value of range



Solved Question 1 Let F X Sin 1 X 2 Then The Second Derivative At X 1 F 1 Equals A 2 3sqrt3 B 1 4sqrt3 C 2 Sqrt39 D Sqrt6 9 E Course Hero




Increasing And Decreasing Function Ppt Download
1 f X(y 1 n) where, f X() is the pdf of X which is given Here are some more examples Example 1 Suppose Xfollows the exponential distribution with = 1 If Y = p X nd the pdf of Y Example 2 Let X ˘N(0;1) If Y = eX nd the pdf of Y Note Y it is said to have a lognormal distribution Example 3 Let Xbe a continuous random variable with pdf f⇒ f (x) will be increasing for 1 ≤ x < 2 and will have the least value at x = 1 for the considered interval ⇒ f ( 1 ) = 1 1 2 2 = 1 3 = 3 C a s e 2 − Taking 2 ≤ x < 3 ,> 1 Taylor polynomials > 11 The Taylor polynomial Let f(x) be a given function, for example ex,sinx,log(x) The Taylor polynomial mimics the behavior of f(x) near x= a T(x) ≈f(x), for all x"close" to a Example Find a linear polynomial p 1(x) for which ˆ p 1(a) = f(a), p0 1 (a) = f0(a) p 1 is uniquely given by p 1(x) = f(a)(x−a)f0(a) The graph of y= p



Scottmccracken Weebly Com Uploads 9 0 6 6 Continuity Print Version Pdf



Users Math Msu Edu Users Yanb Chapter5 Pdf
Transcript Ex 12, 9 Let f N → N be defined by f (n) = { ((𝑛 1)/2 ", if n is odd" @𝑛/2 ", if n is even" )┤ for all n ∈ N State whether the function f is bijective Let f(x)=tanx/x, then log(lim x tends to 0 (f(x)x 2) 1/{f(x)}) is equal to, (where denotes greatest integer function and{} fractional part)=???In mathematics, an injective function (also known as injection, or onetoone function) is a function f that maps distinct elements to distinct elements;



2



Let F X X 2 1 X 2 And G X X 1 X X R 1 0 1 If H X F X G X Then The Local Minimum Value Of H X Is Sarthaks Econnect Largest Online Education Community
(a) For any constant k and any number c, lim x→c k = k (b) For any number c, lim x→c x = c THEOREM 1 Let f D → R and let c be an accumulation point of D Then lim x→c f(x)=L if and only if for every sequence {sn} in D such that sn → c, sn 6=c for all n, f(sn) → L Proof Suppose that lim x→c f(x)=LLet {sn} be a sequence in D which converges toc, sn 6=c for all nLet >0To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Let f(x)=x1x1Then f is differentiable inAnswer to Let f(x) = \dfrac{x^2 3x 2}{x 1} State any inflection points By signing up, you'll get thousands of stepbystep solutions to




Let F X 1 1 X 2 Then Range F




Integral Wikipedia
Example \(\PageIndex{1}\) Let the random variable \(X\) denote the time a person waits for an elevator to arrive Suppose the longest one would need to wait for the elevator is 2 minutes, so that the possible values of \(X\) (in minutes) are given by the interval \(0,2\)X!af(x), we can derive many general laws of limits, that help us to calculate limits quickly and easily The following rules apply to any functions f(x) and g(x) and also apply to left and right sided limits Suppose that cis a constant and the limits lim x!a f(x) and lim x!a g(x) exist (meaning they are nite numbers) Then 1lim x!af(x) g(x1 2, but if we let x ˘ 1 n2 for some n ‚k then the left side is at least 1/2, generating a contradiction The other cases follow similarly By Theorem 712, f is continuous on intervals where it converges uniformly, which in this case happens to include the set of sets where it converges pointwise Lastly, we prove that f is not bounded Let




D L L 96 Let F X X2 6x 5 X 5x 6 Iit Jee 2 Math
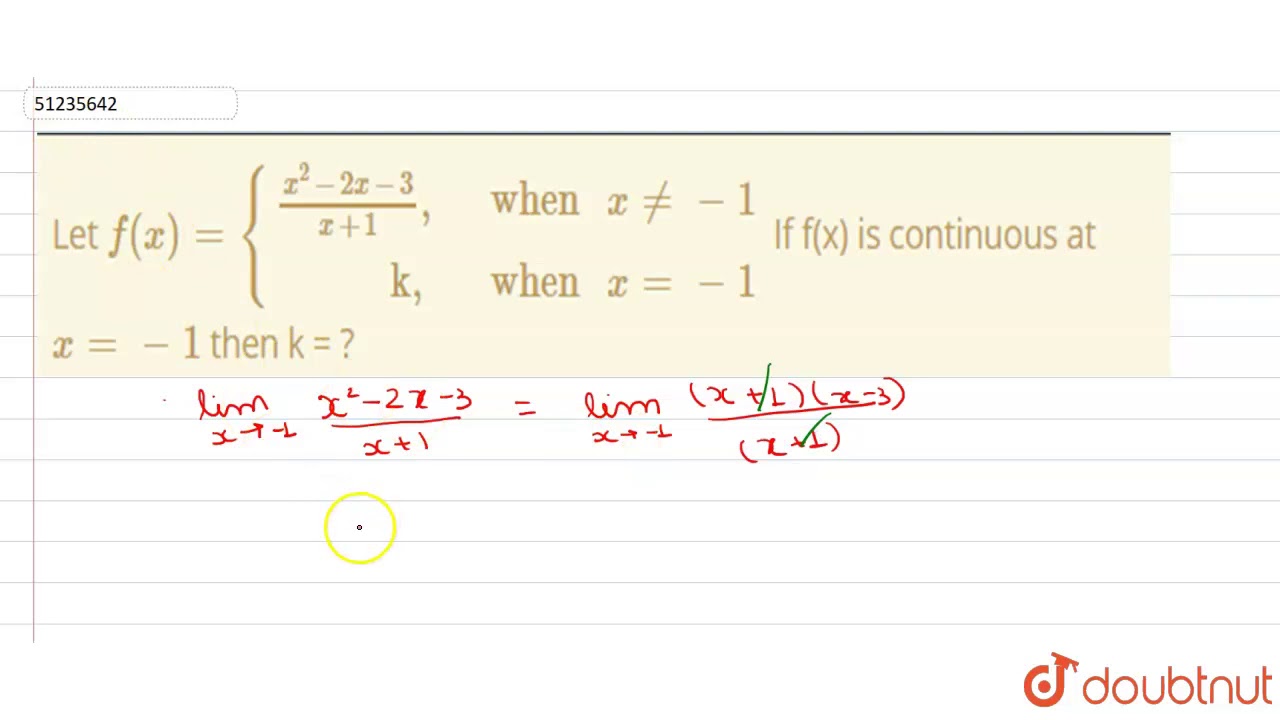



Let F X X 2 2x 3 X 1 When X 1 K When X 1 Youtube
Let f(x) = e x – x and g(x) = x 2 – x, ∀ x ∈ R Then the set of all x ∈ R where the function h(x) = (fog)(x) is increasing, is A \(\left { 1,\frac{{ 1}}{2}} \right \cup \left {\frac{1}{2},\infty } \right)\)Then , `f (f(x))` = 1 (1 x ) = 2 x ∵ 1 ≤ f (x) < 2 When ,1 < x ≤ 2 Then , f (x) = 1 x Now when , 1 < x ≤ 2 then,2 < x 1 ≤ 3 Then , f (f(x)) = 3 − ( 1 x ) = 2 − x ∵ 2 ≤ f(x)Then X is approximately N(np,np(1 − p)) • Rule of thumb this approximation is reasonably good for np(1 − p) > 10 • P(X = k) ≈ P(k − 1/2 < Y < k 1/2) where Y ∼ N(np,np(1 − p)) • Note P(X≤ k) is usually approximated by P(Y < k 1/2) 25



If 2f X F 1 X X Then What Is F X Quora




Let F X X 1 X 1 Then F F X Is A 1 X B 1 X C 1 X 1 D 1 X 1 Brainly In
F (x) ˘ X1 n˘1 cnI(x¡xn) (a •x •b) converges uniformly, and that f is continuous for every x 6˘xn Solution Let fk(x) ˘ Xk n˘1 cnI(x¡xn) By the Weierstrass Mtest (Theorem 710) with Mn ˘jcnj, {fk(x)} converges uniformly to f (x) Let E ˘ a,b\{xn n 2 N} Since each fk(x) is continuous on E, then by Theorem 712 we know that fTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If` 2f(x)3f(1/x)=x^21` then `f(x)` is2 (a) Define uniform continuity on R for a function f R → R (b) Suppose that f,g R → R are uniformly continuous on R (i) Prove that f g is uniformly continuous on R (ii) Give an example to show that fg need not be uniformly continuous on R Solution • (a) A function f R → R is uniformly continuous if for every ϵ > 0 there exists δ > 0 such that f(x)−f(y) < ϵ for all x




Let F X X Root 1 X2 Show That Fofof X X Root 1 3x2 Brainly In




10 Let F X X2 X 1 Its Derivative Chegg Com
That is, f(x 1) = f(x 2) implies x 1 = x 2 In other words, every element of the function's codomain is the image of at most one element of its domain 2 Let f (x) = { (1 cos 4x)/x^2, if x < 0 and a, if x = 0 and x/ (√ (16 √x) 4), Let f (x) = { (1 cos 4x)/x2, if x < 0 and a, if x = 0 and √x/ (√(16 √x) 4), if x > 0} If f (x) is continuous at x = 0, determine the value of a Please log in or register to add a comment Let the functioin 'f' be defined by f (x) = 5x² 2 ∀ x ∈ R, then 'f' is (a) onto function (b) oneone, onto function (c) oneone, into function (d) manyone into function Answer Answer (d) manyone into function



How To Prove That F X X Sqrt X 2 1 Is Injective Quora




Let F X Be A Polynomial Function If X Is Divided By X 1 X 1 X 2 Then Remainders Youtube
Click here👆to get an answer to your question ️ Let f(x) = x^2 1x^2 and g(x) = x 1x, x ∈ R { 1, 0, 1 } If h(x) = f(x)g(x) , then the local minimum value of h(x) is Join / LoginTimes If the coin lands tails, you roll the die 101 times Let X be 1 if the coin lands heads and 0 if the coin lands tails Let Y be the total number of times that you roll a 6 Find P(X = 1Y = 15) We can find P(X = 1Y = 15) using Bayes' Rule It's easiest using the "odds" form P(X = 1Y = 15) P(X = 0Y = 15) = P(X = 1)F '(x) = lim h→0 1 (xh)2 − 1 x2 h ∴ f '(x) = lim h→0 1 h ⋅ x2 − (x h)2 (x h)2 x2 ∴ f '(x) = lim h→0 x2 −(x2 2hx h2) h(x h)2x2 ∴ f '(x) = lim h→0 x2 − x2 −2hx − h2 h(x



Let F X Bsin 1 X C 2 1 2 X 0 1 2 X 0 E Ax 2 1 X X X 1 2 Sarthaks Econnect Largest Online Education Community



2
F (a) 2 (x −a)2 Check that P 2(x) has the same first and second derivative that f (x) does at the point x = a 43 Higher Order Taylor Polynomials We get better and better polynomial approximations by using more derivatives, and getting higher degreed polynomials The Taylor Polynomial of Degree n,forx near a is given by P n(x) = f (a) f In finding the limit, we'll need to consider the left and right limits separately because the rule changes at x = 1 The limit from the right is lim x→1 f (x) = (1)2 = 1 The limit from the left is lim x→1− f (x) = 2(1) = 2 Because the right and left



Www3 Nd Edu Apilking Math Work Old exams Exam 3f12 Sols Pdf




Let F X 1 X 0 X 2 3 X 2 Lt X 3 Then Find Fof Fof Means Brainly In



Let F X X For 0 X 2 1 For X 0 Then X 0 Has




8 Let F X Log X Sqrt X 2 1 Then F Prime X Equals Begin Array Ll Text 1 Sqrt X 2 1 Text 2 Frac X Sqrt X 2 1 Text 3 1 Frac X Sqrt X 2 1 Text 4 Frac 1 Sqrt X 2 1 End Array




Let F X Ln 1 X Use A Linearization To Estimate In 2 Explain Clearly What Homeworklib




Section 2 7 One To One Functions And Their Inverses Pdf Free Download



Let A R 2 B R 1 If F A B Is A Function Defined By F X X 1 X 2 Show That F Is One One Onto Sarthaks Econnect Largest Online Education Community




Is G 1 1 2 3 3 5 4 7 A Function If This Is Described By The Formula G X Alpha X Beta Then What Values Should Be Assigned To Alpha And Beta



Www Math Ucla Edu Azhou Teaching 19s 131 Hw 08 Sols Pdf




Let F R R Be A Function Is Defined By F X X 2 X 2 1 X 2 Then



Courses Math Tufts Edu Math32 Exams Sol2 F07 Pdf



Www Ma Imperial Ac Uk Ruzh Papers Additional Pdf



Http Www Math Ust Hk Machiang 1 Chiang Wksht Week10 Sol Pdf
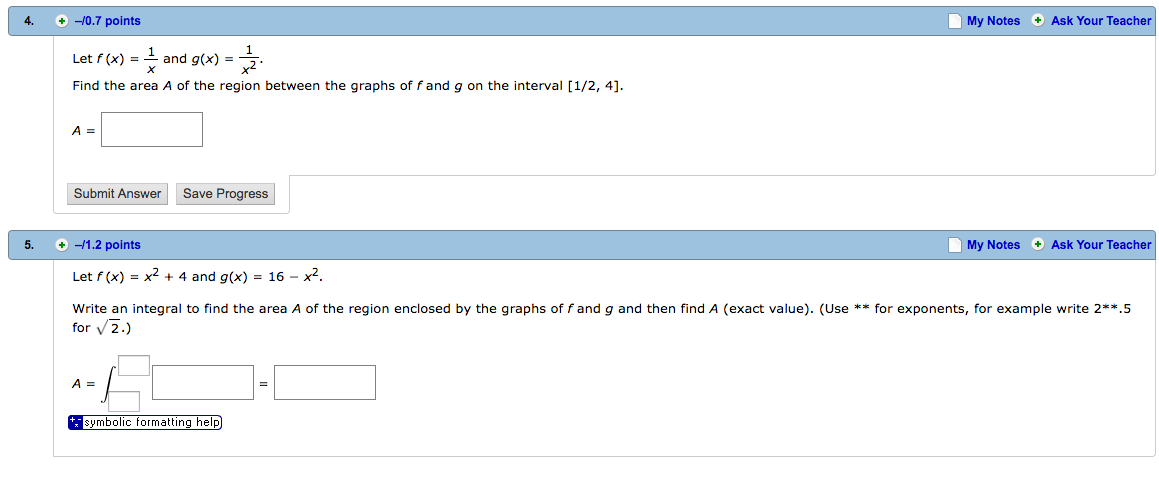



Let F X 1 X And G X 1 X 2 Find The Area A Of Chegg Com



Www3 Nd Edu Apilking Math Work Old exams Exams s13 M final sp13 solution Pdf



Http Maths Dur Ac Uk Dma0wjz B1 Anlec1 Pdf



2
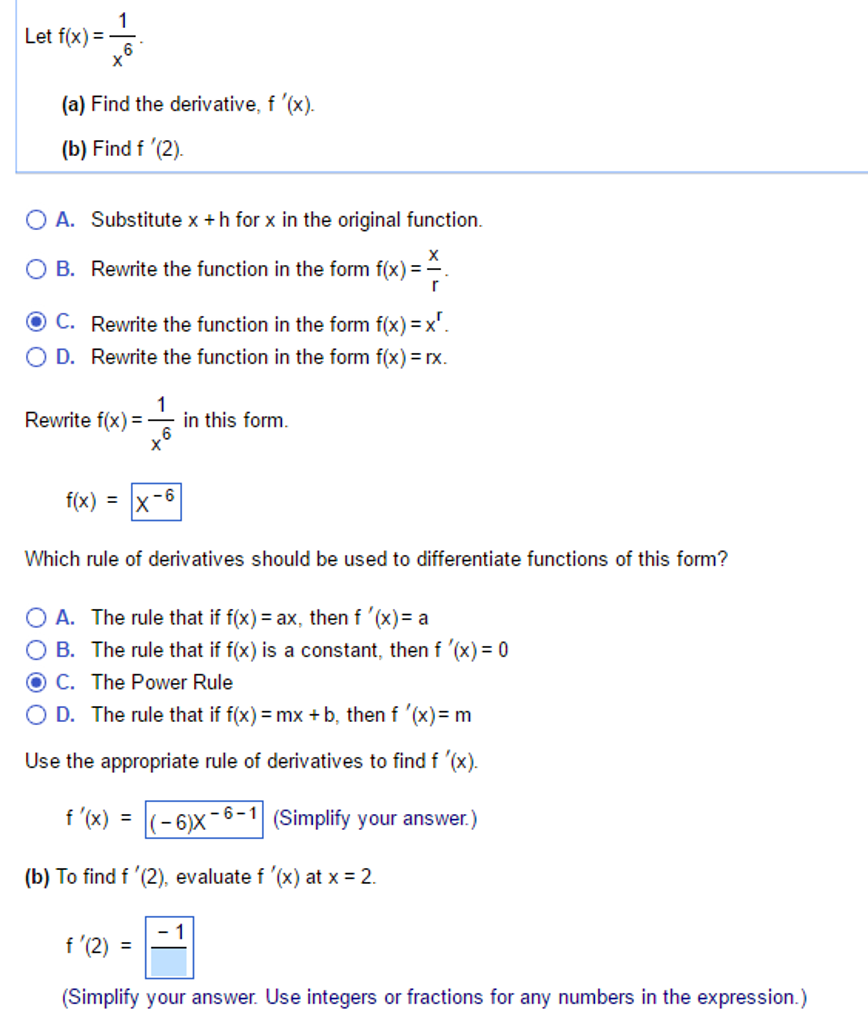



Let F X 1 X 6 Find The Derivative F X Find Chegg Com



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 4 Pdf




If F R R Be Defined By F X X 2 1 Then Find F 1 17 And F 1 3




Let F N N Be Defined By F X X 2 X 1 X N Then F Is




Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G
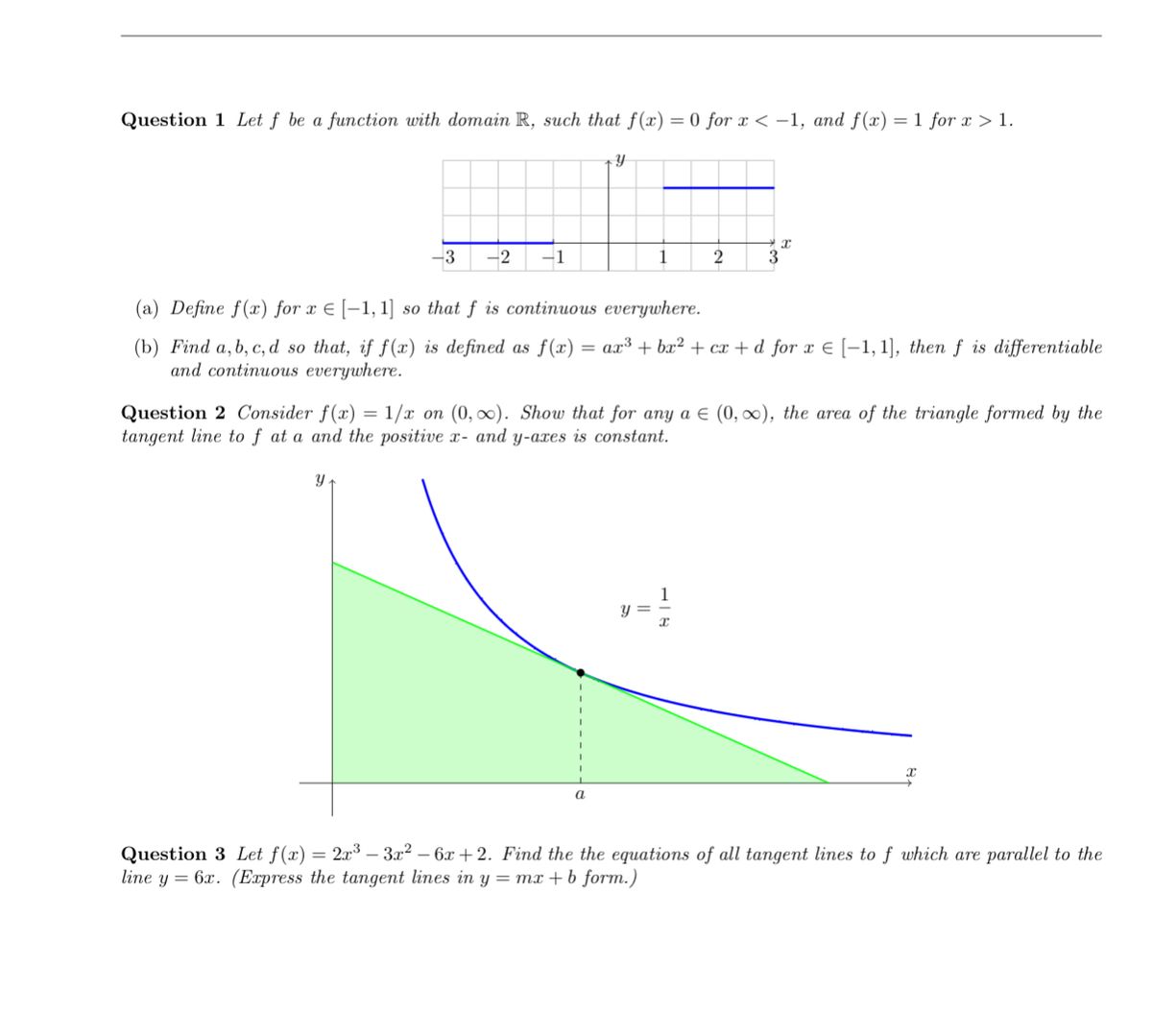



Answered Question 1 Let F Be A Function With Bartleby




If F Is A Real Function Satisfying F X 1 X X2 1 X2 For All X E R 0 Then Write Maths Relations And Functions Meritnation Com




Determine The Domain Of Each Function F X 6x 7 Chegg Com



Let F X X 2 1 X 2 And G X X 1 X X R 1 0 1 If H X F X G X Then The Local Minimum Value Of H X Is Sarthaks Econnect Largest Online Education Community




Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G



2



12 6 Arc Length




If The Function F X X 2 1 X 1 When X 1 K When X 1



G X Graph



If 2f X F 1 X X Then What Is F X Quora




Let F X Sin X 1 X 2 Let Y N Denote The N Th Derivative Of F X At X 0 Then The Value Of Y 100 9900y 98 Is Wyzant Ask An Expert




Let F X Root X 1 Root X 2 Then F 2 Is Equal To Brainly In



Http Www Webassign Net Resources Rogacalcet2 Chap04 Et Student Solutions 2e Pdf



Let F X X 2 1 X 2 2 If X 1 If X Less Than And Quizlet




Inverse Functions And Logarithms Pdf Free Download




Let F X Log X Sqrt X 2 1 Then F X Equals Youtube



psrohini Balbharati Org Wp Content Uploads 21 06 Mathematics Today May 21 1 Pdf
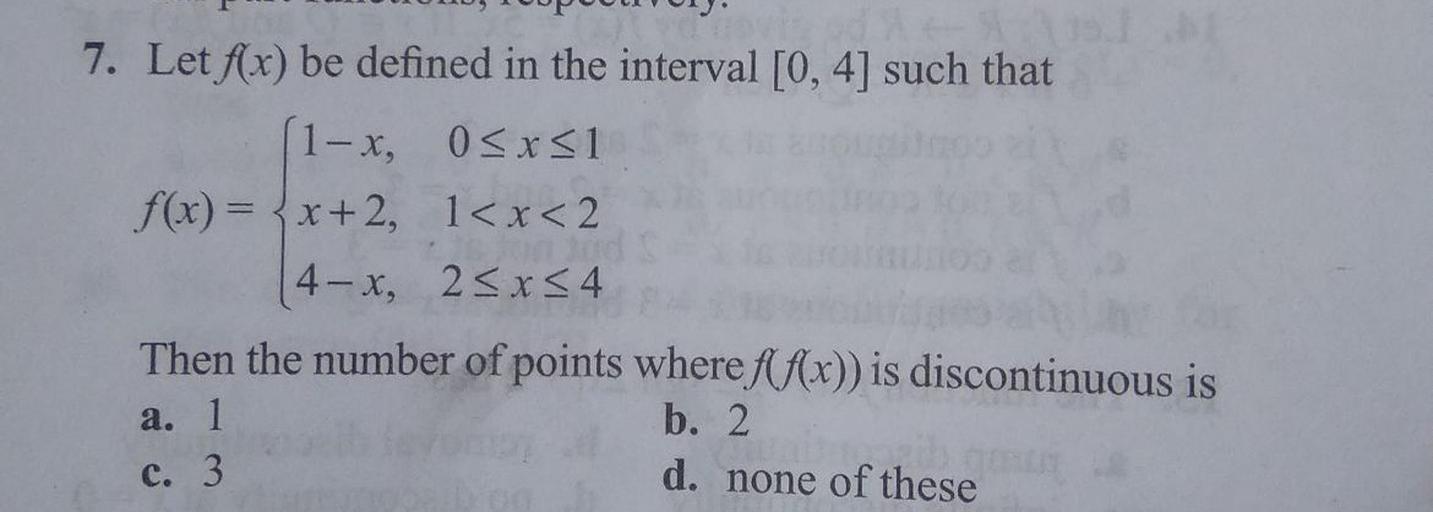



7 Let F X Be Defined In The Interval 0 4 Such That Math



Www Geneseo Edu Johannes Gre practice problems Pdf



Http Www Maths Usyd Edu Au Math1921 R 18s1 Pdf Tut10s Pdf



Composite Functions




Misc 2 If F X X2 Find F 1 1 F 1 1 1 1 Chapter 2




If F X 1 X 1 X Show That F X F X 2 1 F X 2 1 2 Maths Relations And Functions Meritnation Com




Question 5 Let Fx 1 X Then F X X2 True False Gauthmath
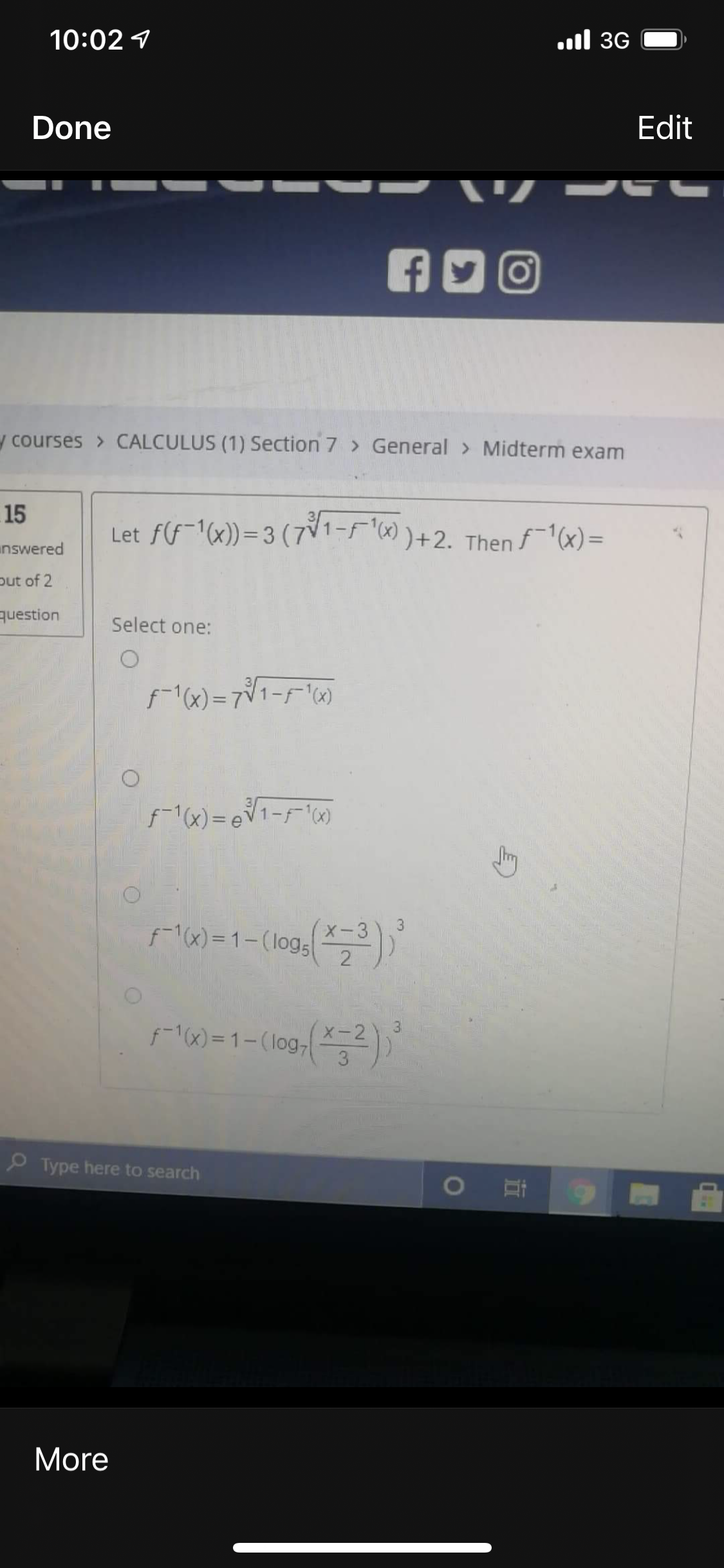



Answered Let F F 1 X 3 71 F 2 Then Bartleby




Let Fx X2 1 X R Then F 3 F 2 5 5 15 15 Gauthmath




Let Fx X3 Be Defined On 0 1 Find The Left Rig Gauthmath



Eml Berkeley Edu Cshannon E4 11 Lecture13 Pdf



Solved Question 1 Let F X Sin 1 X 2 Then The Second Derivative At X 1 F 1 Equals A 2 3sqrt3 B 1 4sqrt3 C 2 Sqrt39 D Sqrt6 9 E Course Hero




Relations Functions Pps



Www Csus Edu Indiv B Binlu M130a Hw8sol Pdf




Solving Polynomial Equations Answers




Given The Function F X 1 X 2 Find The Points Of Discontinuity Of The Composite Funtion Y F F X Maths Continuity And Differentiability Meritnation Com



2




Mc Ex 1 4 Unit 4 Formulae Polynomials And Algebraic Fractions



Given F X 8x 3 3x How Do I Find F 1 X Quora



Exercise I Jee Main Hcl Learning Flip Ebook Pages 1 10 Anyflip Anyflip



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 Ch4sol Pdf




Let F X Be A Polynomial Function If F X Is Divided By X 1 X 1 X 2 Then Remainders Are 5 3 And 2 Respectively When F X Is Divided By X 3 2 X 2 X



Http Www Math Ucsd Edu Tiz161 Solution280b Pdf




Let F X X 1 X 2 And G X E X 1 X Where Denote Greatest Integer Function Then



2




Let F X 1 X X 2 1 X 2 X Ne 0 Then F X Equals



Let F X E X X 1 X 2 Dx Then F Decreases In The Interval Sarthaks Econnect Largest Online Education Community




Inverse Functions And Logarithms Pdf Free Download



1




Sample Exam 1



2




Misc 2 If F X X2 Find F 1 1 F 1 1 1 1 Chapter 2




Let F X X 2 X 2 X 2 X 1 X 2 X Chegg Com




Polynomial Wikipedia




Let F X X 1 X 1 Then F Is Differentiable In Youtube



Www3 Nd Edu Math Restricted Coursearchive 100level 126 f f Stanton Quizzes Exam1 Sol Pdf



Www Ualberta Ca Rjia Math214 Hwks Sol9 Pdf



Fog X




Let F X X 1 2 1 X 1 Then The Set X F X F 1 X



0 件のコメント:
コメントを投稿